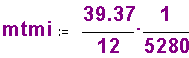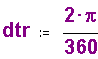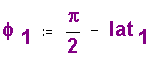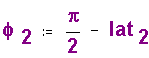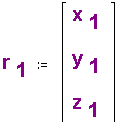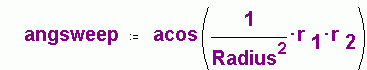A woman armed with a ham radio reporting on her experiments and experiences
A (somewhat) New Ham Radio Operator Blogging and Slogging Along
CALCULATING GREAT CIRCLE DISTANCES
On this page I will show the vector methods for calculating the distance along a Great Circle arc, from one location to another.
|
Construct conversion factor for converting meters to miles: |
||
|
|
|
|
|
Radius of Earth: |
|
|
|
Radius of Earth converted to miles: |
|
|
|
Circumference Earth (just to check) |
|
|
|
Construct conversion factor for converting degrees to radians: |
||
|
|
|
|
|
My home location and converting to radians |
||
|
|
|
|
|
|
|
|
|
Location in Indianna, and converting to radians |
||
|
|
|
|
|
|
|
Convert latitude and longitude into Theta and Phi in a polar spherical coordinate system |
||
|
Theta is measured in the Equatorial plane, from an X axis at the GMT meridian. |
||
Since longitude is measured from that same meridian, Theta is the same as longitude. |
||
|
|
|
|
|
|
|
|
Phi is measured from the North Polar axis. Since latitude is measured from the Equator, |
||
|
Phi is 90 - Latitude. | ||
|
|
|
|
|
|
|
|
Write equations for X Y and Z in polar spherical coordinates, for both locations, and calculate their values |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In Mathcad, vectors look like vertical matices, having one column and three rows. | ||
|
|
|
|
|
|
|
|
|
The dot product of two vectors is equal to the product of their two magnitude and the cosine of the angle between the two vectors. Calculate the dot product of the two position vectors: |
||
|
|
||
|
Divide this by the magnitudes of the two vectors, (which are both magnitude Radius of
the Earth), (This comes out in Radians) | ||
|
|
|
|
|
The distance along an arc swept out by a vector, as it sweeps through an angle from it's
own location, to the location of the other position vector, is equal to the angle in radians multiplied by length of the vector |
||
|
I named the distance along the arc, "GCdist" which stands for "Great Circle Distance." | ||
|
|
| |
|
Or: 1,798.4 Miles |
||
|
This agrees with what is given in the QRZ.com amateur radio operator database. This answer is 0.2 miles different (out of 2000 miles) so this is approx a 0.01% difference. |
||
|
Comments on anything at this website? Please go to the COMMENTS page using the link further down this page. After submitting your comment there, find and click on the link on that page which enables you to return to the main page. |